小数の計算はミスが発生しやすい単元です。点を打つ位置をうっかり間違えてしまい、減点された経験はありませんか。小数の計算はルールをしっかりと理解し、その上でケアレスミスに気をつけながら臨む必要があります。
この記事では、小数のかけ算についてわかりやすく紹介します。
そもそも小数ってなに?

そもそも小数とはどんな数なのでしょうか。
小数は1より小さな数を表す
小数は、1より小さな数を表すときに使います。たとえば、1kg分のお菓子を10人で分けたとしたら一人分は0.1kg、100人で分けたとしたら一人分は0.01kg、1000人で分けたら一人分は0.001kgと表すことができます。
小数第一位ってなに?
小数を表すときに使う点を小数点といいます。小数点の左側が整数部、右側が小数部です。小数点のすぐ右に続く数字を小数第一位といい、小数第二位、小数第三位と続きます。
たとえば、23.847という数字があったら、整数部は23で、小数部が847です。この場合、小数第一位が8、小数第二位が4、小数第三位が7になります。
小数と分数の関係って?
小学校では1より小さな数を表すときに分数も使います。小数と分数は以下のようにイコールで結ぶことが可能です。
| 0.1 | = | 1 |
| 10 |
| 0.01 | = | 1 |
| 100 |
| 0.001 | = | 1 |
| 1000 |
分数を小数に置き換えたり、小数を分数に置き換えたりして解く問題もあります。
小数のかけ算ってどう解くの?

小数のかけ算の解き方を見ていきましょう。
小数と整数のかけ算
小数と整数のかけ算はどのように解けばよいのでしょうか。
小数を10倍、100倍、1000倍、10000倍にする計算をしてみよう
以下の式を見てください。
1を10個に分けたうちのひとつが0.1なので、0.1を10倍すれば1になりますね。
続いて、以下の式を見てください。
0.1 × 100 = 10
0.1 × 1000 = 100
0.1 × 10000 = 1000
0.1に10をかけると、0.1の小数点が1つ右に移動します。
0.1に100をかけると、0.1の小数点が2つ右に移動します。
0.1に1000をかけると0.1の小数点が3つ右に移動します。
0.1に10000をかけると0.1の小数点が4つ右に移動します。
要するに、小数を10倍、100倍、1000倍(以下略)にするかけ算の場合、整数の0の数だけ小数点を右に移動させると答えになります。
まとめると以下のように0の数と小数点の移動が対応しています。
逆に「整数の小数点を左に移動」という考え方もできますね。「整数に小数点?」と疑問に思うかもしれませんが、たとえば1は1.0を意味しますし、2は2.0、100は100.0です。
そして、0.1は後ろから数えて小数点は1つ目です。
10は「10.0」、100は「100.0」、1000は「1000.0」、10000は「10000.0」のことですから、小数点が隠れているものと考え、それを移動させるやり方です。
整数同士で計算してから小数点を移動させよう
ここまではかける数が10や100といったわかりやすい数だったので簡単でした。
では、0.1 × 12といった計算はどのように解けばよいのでしょうか。
0.1は1を10こに分けたうちのひとつです。
つまり1が12こあれば12ですが、0.1が12あると1.2になります。このあたりがパッと理解できる人は小数の暗算も得意かもしれませんね。解く際の手順としては以下のとおりです。
0.1の小数点を右にひとつずらして整数の1にする。1×12=12
計算するにあたり、小数の小数点を右に1つずらしたので、その分を元に戻すと1.2になります。
0.01の小数点を右に2つずらして整数の1にする。1 × 12 = 12
小数点を右に2つずらしたので、その分を元に戻すと0.12になります。
0.001の小数点を右に3つずらして整数の1にする。1 × 12 = 12
小数点を右に3つずらしたので、その分を元に戻すと0.012
になります。
基本の小数。例題を解いてみよう
ここまで見てきたように、小数は一度整数に戻して計算するとわかりやすいです。それでは以下の計算を試してみましょう。
① 0.2 × 12
② 0.03 × 12
③ 0.004 × 12
0.2の小数点を右に1つずらして整数の2にする。2 × 12 = 24
小数点を右に1つずらしたので、その分を元に戻すと2.4になる。
0.03の小数点を右に2つずらして整数の3にする。3 × 12 = 36
小数点を右に2つずらしたので、その分を元に戻すと0.36になる。
0.004の小数点を右に3つずらして整数の4にする。4 × 12 = 48
小数点を右に3つずらしたので、その分を元に戻すと0.048になる。
自力で解けたなら、小数のかけ算の基本は大丈夫です。次のステップに進みましょう。
小数のひっ算の解き方を覚えよう
小数をひっ算で解くにはどうすればよいのでしょうか。
複雑な計算はひっ算で解く
ここまでで出てきた計算のように単純なものであれば、ひっ算は必要ないでしょう。しかし、複雑な計算になってくるとひっ算を使わないで解くのは難しくなります。
たとえば、3.6 × 4.5 の場合、以下のようなひっ算になります。
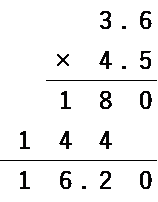
36 × 45の計算をして、小数点を書き加えます。3.6と4.5はどちらも、後ろから数えて数字1つ分のところに小数点があります。1つ分と1つ分、あわせて数字2つ分です。答えには2つ分のところに小数点を書きます。
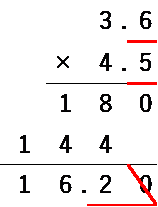
小数の最後の0は基本的に書かなくてよいので、斜線を入れます。
足し算のやり方と混同しない
よくありがちなミスとして「たし算のやり方で小数点を打ってしまう」というものが挙げられます。以下のたし算を見てください。
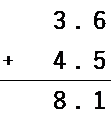
たし算の場合、ひっ算では小数点の位置を揃えて計算します。そのため式と答えの小数点は同じ位置にきます。かけ算は足し算とは違うので注意しましょう。
単位変換の問題でも小数のかけ算は大活躍

小数のかけ算をよく使う問題に、単位変換があります。
水量や重さ、距離の問題で単位を変換する際、どのように小数が必要になるのか見ていきましょう。
重さの問題を解いてみよう
たとえば、「1kg500gをkgで表してください」という問題が出たとします。答えは1.5kgですが、この答えを書けるようになるには500g = 0.5kgとすぐに出てこなければなりません。
まず、1kgが1gの1000倍であることを理解してください。
1g = 1kg ÷ 1000
です。つまり1gとは0.001kgとイコールになります。
500gは1g(0.001kg)の500倍なので、0.5kgです。
それでは、次の例題を試してみましょう。
① 4kg200gをkgで表してください。
② 125gをkgで表してください。
③ 2kg10gをkgで表してください。
4kgはすでに単位がkgなので、問題ありません。考えなければならないのは200gです。kgはgの1000倍なので、1gは0.001kgです。
つまり200gは0.001kgの200倍で、0.001 × 200 = 0.2kgになります。したがって、4kg + 0.2kg = 4.2kgです。
1kgが1000gということは、1gは1kg ÷ 1000 = 0.001kgです。
よって125gは0.001 × 125 = 0.125kgといえます。
2kgはすでに単位がkgなのでそのままで問題ありません。考えなければならないのは10gが何kgになるかです。
1gが0.001kgなので、10gは0.001 × 10 = 0.01kgとなります。よって答えは2.01kgです。
こうした基本が理解できたところで以下の問題を解いてみましょう。
① 100gの箱を5個用意しました。全部で何kgでしょうか。
② 一箱0.5kgのお菓子を30箱買いました。全部あわせて何gでしょう。
100g × 5箱は500g
1kg = 1000gのため、500gは0.5kgです。
0.5kg × 30 = 15kg
1kg = 1000gなので、15kgは15000gです。
水量の問題を解いてみよう
次に水量の問題を解いてみましょう。水量の問題はL、dl、mlなどの単位をよく使います。
1Lは1000mlであり、10dlでもあります。つまり1dlは100mlともいえます。
1L = 10dl
1dl = 100ml
しっかり覚えて計算で間違えないようにしましょう。
それでは、以下の問題を解いてみましょう。
① 0.1L × 3 = □dl
② 0.3dl × 4 = □ml
② 150ml × 5 = □L
0.1L × 3 = 0.3Lです。1L = 10dlですから、0.1Lだと1dlになります。
つまり、0.3Lは3dlになるのです。
0.3dl × 4 = 1.2dlです。1dl = 100mlですから、1.2dl = 120mlとなります。
よって120mlです。
1000ml = 1Lですから、150mlは0.15Lです。
0.15 × 5 = 0.75Lとなります。
距離や長さの問題を解いてみよう
距離や長さの問題もよく出ます。km、m、cm、mmなどの単位は、子供にとって馴染みのあるものでしょう。
まずは以下の基本的な単位変換を覚えましょう。
1m = 100cm
1cm = 10mm
覚えたら、問題を解いてみましょう。
① 210m × 4 = □km
② 35cm × 10 = □m
② 家と公園とスーパーは直線上に位置しています。家から公園までの距離が100m、公園から駅までの距離が730mです。家から公園を通ってスーパーまで行き、再び家に戻った場合の距離をkmで答えてください。
1000m = 1kmなので210m = 0.21kmです。0.21 × 4 = 0.84kmとなります。
100cm = 1mなので、35cm = 0.35mです。0.35 × 10 = 3.5mとなります。
家から公園までの距離は100mで、公園から駅までの距離は730m。あわせて830mで、往復だと2倍です。
1km = 1000mですから100m = 0.1km。730mは0.73kmです。
つまり片道は0.1km + 0.73kmで0.83kmです。往復となると、それが二倍ですから0.83km × 2で1.66kmになります。
小数のかけ算の細かなルールを覚えよう
小数のかけ算には小数点を書く場所をはじめ、さまざまなルールがあります。ケアレスミスを防ぐためには、複雑な問題ではひっ算を用い、一度整数に戻して計算をするとよいです。整数の答えを一旦導き出してから、小数点を正しい位置に書き込めるようになりましょう。
小数の単元では、難しい計算もたくさん扱います。その際に多いケアレスミスが、他の計算ルールとの混同です。とりわけ、小数点を打つ位置を間違えて大幅に点を落とすような事例はよく見ます。
単位変換の問題でも小数は必要です。重さや水量、距離・長さの問題がよく出ます。単位変換は基準をしっかり覚えておきましょう。
小数の計算は今後もさまざまな単元で必要となります。文章題で計算ミスをして大きく失点する子供も多いです。式を書くときには、点の位置を何度か見直すクセをつけることをおすすめします。