表面積ってなに?
円すいの表面積(ひょうめんせき)とは、外から見えるすべての面のひろさのことです。
円すいは次の2つの部分からできています。
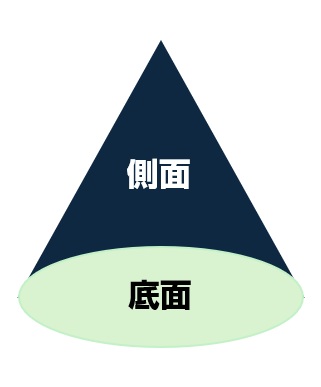
- 底面(ていめん):まるい円の部分
- 側面(そくめん):ななめになっている面
この2つの面のひろさを足すと、「表面積」になります。
覚えよう!円すいの表面積の公式
まずは公式のおさらいから始めます。
表面積の公式はこちら!
表面積 = 底面積 + 側面積= 半径 × 半径 × 3.14 + 母線 × 半径 × 3.14
図で見てみよう!
円すいの見取図
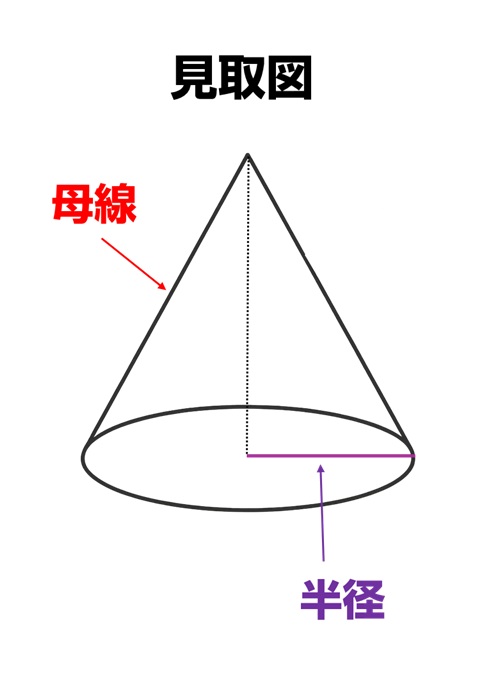
円すいの展開図
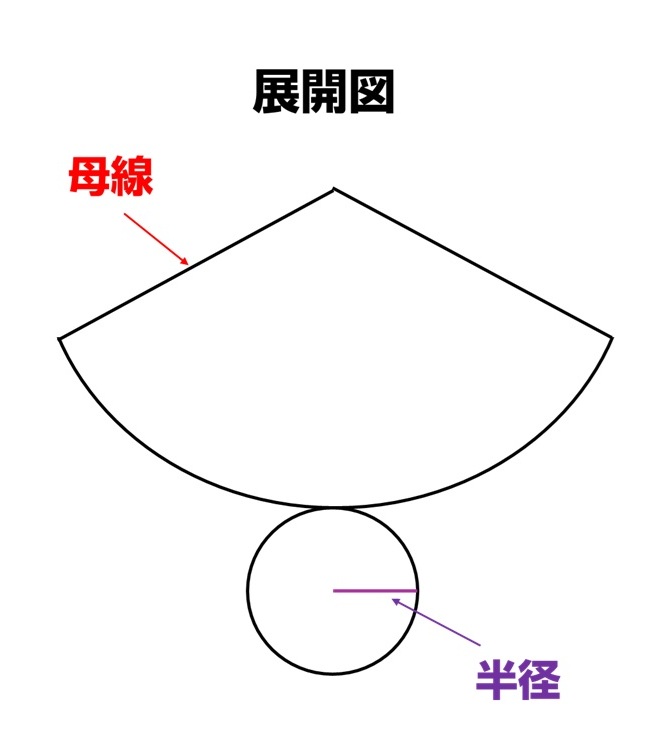
かんたんな例題にチャレンジ!
今回は2種類の例題を紹介します。
底面の半径がわかっている問題
例題1:半径が5cm、母線が10cmの円すいの表面積を求めなさい。
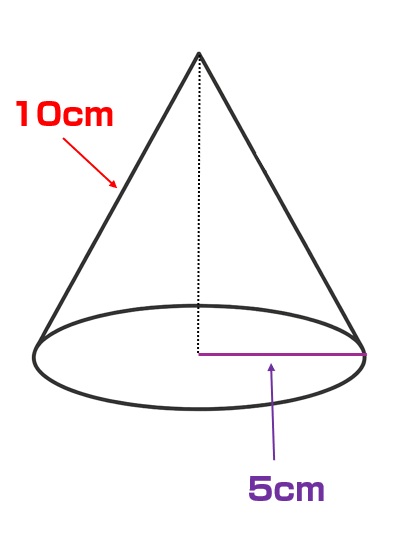
底面積をもとめる計算
5 × 5 × 3.14= 78.5
側面積をもとめる計算
5 × 10 × 3.14 = 157
足し算
78.5 + 157 = 235.5
▶ 答え:235.5cm²
おうぎ形の面積と中心角から求める問題(側面積を求める近道問題)
例題2:半径10cm、中心角216°のおうぎ形を丸めて円すいを作りました。この円すいの表面積を求めなさい。
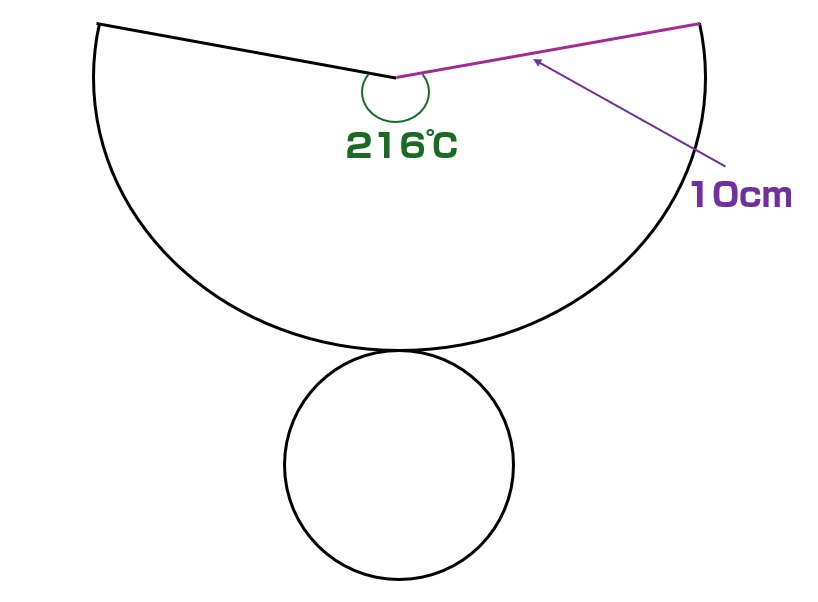
解説
おうぎ形の半径は、円すいの母線に等しいので、母線は10cmです。おうぎ形の中心角が分かれば円すいの底面の半径を求めることができます。中心角が216°のおうぎ形の弧の長さは、底面の円周と等しいです。
おうぎ形の弧の長さの計算
おうぎ形の弧の長さ=おうぎ形の直径×3.14×(中心角/360)
円周=円の直径×3.14
これらが等しいので、おうぎ形の直径×3.14×(中心角/360)=円の直径×3.14
よって、円の直径=おうぎ形の直径×(中心角/360)
底面の直径=20×(216/360)=12
▶ 答え:12cm
表面積の計算
底面の半径は6cmと分かります。
円すいの表面積は、(底面積) + (側面積) で求められます。
底面積=6×6×3.14=113.04(cm²)
側面積=10×10×3.14×(216/360)=188.4(cm²)
おうぎ形の中心角と半径が分かれば、円すいの底面の半径と母線が分かり、表面積を求めることができます。
これらの例題を通して、様々な条件から円すいの表面積を求める方法を理解しておきましょう。公式をただ覚えるだけでなく、図形の特徴を理解することで、より柔軟に問題に対応できるようになります。
- 半径と直径をまちがえる!
- 母線と高さをまちがえる!(母線はななめ、高さはまっすぐ下)
- 面積なのに cm² をつけわすれる!
円すいの表面積の求め方をマスターしよう!
この記事では、円すいの表面積の求め方について、公式と具体的な計算例を用いて解説しました。底面積は円の面積の公式を使い、側面積はおうぎ形の面積の公式を利用します。おうぎ形の面積と中心角から表面積を求める方法も紹介しました。それぞれの公式と計算方法を理解することで、様々なケースに対応できるようになります。
色々な問題に挑戦して、たのしく図形をマスターしよう★
- 円すいの表面積は「底面積 + 側面積」で求める!
- 母線と半径をつかう公式をおぼえよう!(円の直径=おうぎ形の直径×(中心角/360))
- 図とセットでイメージすると、ぐんとわかりやすくなるよ!