はじめに:時計算ってどんな問題?
時計算がニガテ・・・という人へ。
このページでは、「時計算」ってなに?どう解けばいいの?を小学生にもわかりやすくまとめました!
第1章|時計算の基本ルール
時計算の基礎は「時間の単位変換」と「針の動き」を押さえることから始まります。
時間の単位をしっかり覚えよう
| 単位 | 変換 |
|---|---|
| 1日 | 24時間 |
| 1時間 | 60分 |
| 1分 | 60秒 |
例題を解いてみよう!
問題:3時間15分は何分でしょうか?
答え:195分
計算は3×60+15=195分となります。単位を変えるだけで、複雑そうな問題もシンプルになりますね。
アナログ時計の読み方と針の動き
長い針を長針(分)、短い針を短針(時)といいます。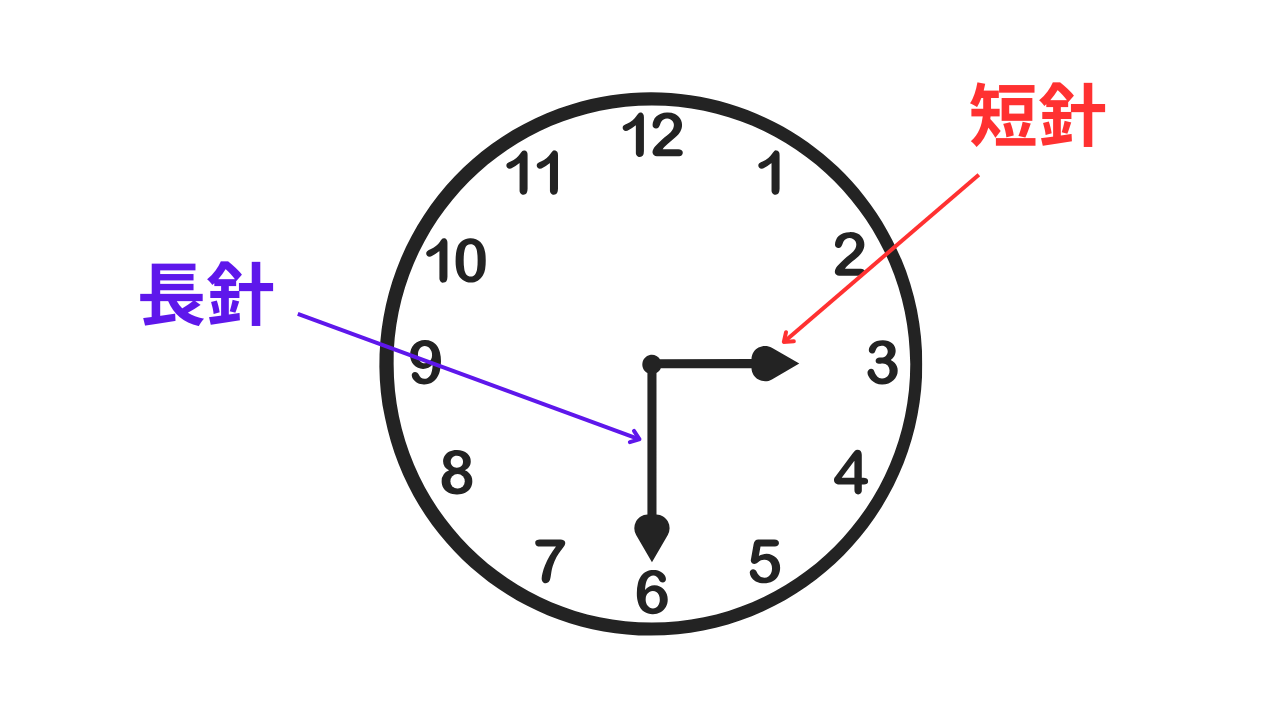
- 長長針(分針)は1分で6度進む
- 短針(時針)は1分で0.5度進む
この性質を覚えておくと、時計の針の角度を求める問題もスムーズに解けるようになります。
第2章|よく出る時計算のパターン
時計算には定番の出題パターンがあります。まずは代表的なものを押さえておきましょう。
時刻の計算(和差算・つるかめ算)
和差算の例題
AさんとBさんが同時に出発し、反対方向に歩きました。2時間後に2人の合計距離は10km。
Aさんは時速3kmで歩いています。ではBさんの速さは?
つるかめ算の例題
午前0時から正午までに、時計の時報は何回鳴るでしょうか?
一言メモ
いずれも「考え方のパターン」を覚えておくと応用が利きます。
時間の単位換算
時間・分・秒の換算も頻出です。特に試験では「単位の間違い」がよくあるミス。比例の考え方を身につけておきましょう。
| 時間 | 分 | 秒 |
|---|---|---|
| 1時間 | 60分 | 3600秒 |
| 2時間 | 120分 | 7200秒 |
通過算(列車・トンネル)
公式はシンプルに距離=速さ×時間です。この公式に当てはめて問題を解いてみましょう。
通過算の例題
問題:長さ100mの列車が秒速20mで鉄橋(長さ50m)を渡ります。渡り終わるまで何秒かかる?
答え:7.5秒
一言メモ
計算は(100+50) ÷ 20 = 7.5となります。公式を応用して答えを導こう。
第3章|ちょっとムズかしい問題のときは?
「文章が長くて混乱する…」そんなときにはダイヤグラムを活用しましょう。ダイヤグラムとは、横軸に「時間」、縦軸に「距離」をとって、動きを線で表したグラフです。
交点を見つければ「出会う時刻」や「追い越す時刻」がわかる仕組み。速さの関係が視覚的に理解できるので、難問にも対応できます。
ダイヤグラム=時間と距離のグラフ
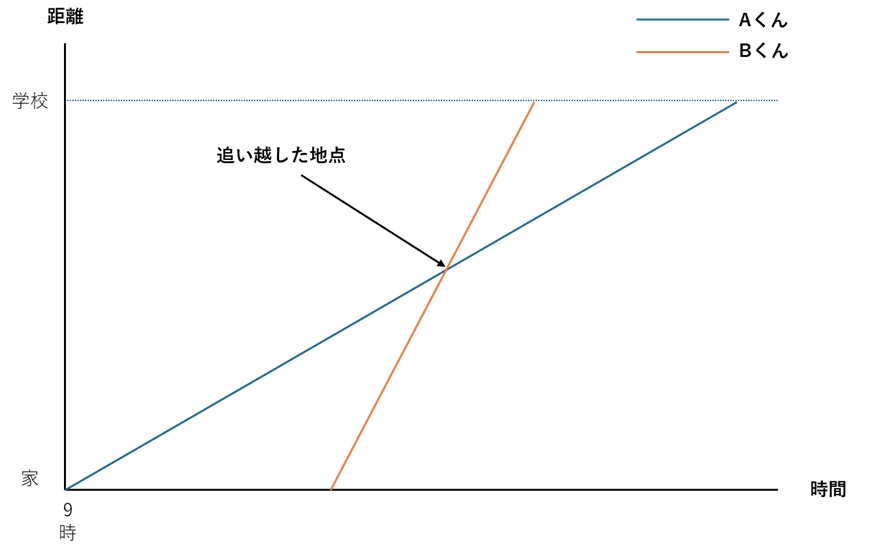
作り方は下記の手順になります。
- 横に「時間」、縦に「距離」をとる
- 物の動きを「線」で表す
- 線の交点が「出会う時刻」「追い越す時刻」
一言メモ
線の角度=速さのヒントだよ!
旅人算とのミックス問題!
| 状況 | ポイント |
|---|---|
| 出会う時刻 | 速さの和を使う |
| 追い越す時刻 | 速さの差を使う |
| 一定時間後に追いつく | 式を立てて解く |
一言メモ
図とダイヤグラムを組み合わせると、スッと解けるよ!
第4章|解法パターンを覚えよう
時計算は「パターンを覚える」と一気に得意になります。
| 問題の種類 | よく使う解法 |
|---|---|
| 時刻の計算 | 和差算・つるかめ算 |
| 単位換算 | 比例式 |
| 通過算 | 距離=速さ×時間 |
| ダイヤグラム | グラフの読み取り |
| 旅人算ミックス | 相対速度(和・差) |
第5章|まちがえたときの復習法

解けなかった問題に出会ったときは、次のステップで復習するのがおすすめです。
- どこで間違えたかをチェック(読みまちがい? 計算ミス? 単位ミス?)
- 正しい解き方を読み直す
- 同じタイプの問題で練習!
- 自分の言葉で説明してみる
一言メモ
「なんでそうなるの?」って声に出してみよう!
おわりに:時計算は「わかる」から「できる」へ!
時計算はただ公式を暗記するだけでは解けません。
「意味を考えながら解く」ことが大切 です。
- 問題をたくさん解こう!
- まちがいを大事にしよう!
- 自分のペースで、少しずつ得意にしよう!
この積み重ねで「時計算が苦手…」が「時計算って得意!」に変わっていきます。
さらに深く学びたい人は、啓林館などの中学受験向け教材や図解つきの問題集もおすすめです。













